normal distribution
Jump to navigation
Jump to search
English[edit]
Noun[edit]
normal distribution (plural normal distributions)
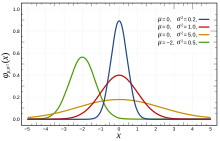
- (statistics) Any of a family of continuous probability distributions such that the probability density function is the Gaussian function
- .
- 2008, James L. Johnson, Probability and Statistics for Computer Science, Wiley, page 437:
- It begins with the normal distribution, which is the limiting form of the sample sum over an arbitrary population.
- 2012, Larry Pace, Beginning R: An Introduction to Statistical Programming, Apress, page 103:
- The normal distribution is the backbone of traditional statistics. We learn very early in our statistics training that the distribution of sample means, regardless of the shape of the parent distribution, approaches a normal distribution as the sample size increases.
- 2014, Mohammad Ahsanullah, B.M. Golam Kibria, Mohammad Shakil, Normal and Student's t Distributions and Their Applications[1], Springer (Atlantis Press), page 7:
- The development of the general theories of the normal distributions began with the work of de Moivre (1733, 1738) in his studies of approximations to certain binomial distributions for large positive integer n > 0.
- Synonyms: (informal) bell curve, Gaussian distribution
Usage notes[edit]
The probability density function is often represented by the Greek letter or .
Derived terms[edit]
Translations[edit]
probability distribution



